Calculo Vectorial : Octubre

MARTES 30 DE NOVIEMBRE

CLASE DE INTRODUCCIÓN A LA MATERIA

El primer día de clases se habló de como se va a llevar la materia este semestre ademas de conocer el texto con el que nos vamos a guiar, también se nos informó que manejaremos un pagina web en la que tendremos que crear nuestros blogs y compartirlos.

En el blog vamos a mostrar las evidencias de lo aprendido en la materia como son los resúmenes diarios de las clases y deberes realizados.

MIÉRCOLES 1 DE OCTUBRE

GEOMETRÍA ANALÍTICA EN 3 DIMENSIONES

Cada función implicita genera una curva en 2 dimensiones y su intersección genera uno o mas puntos.

La recta en el espacio

Dados: a =(l,m,n) y r1 =(x1,y1,z1)

Ecuación vectorial de la recta: r = r1 + t a

Ecuaciones paramétricas de la recta: x = x1+ t (l)

y = y1 + t (m)

z = z1 + t (n )

Ecuaciones simétricas : despejar el parámetro t de las ecuaciones paramétricas.

MARTES 7 DE OCTUBRE

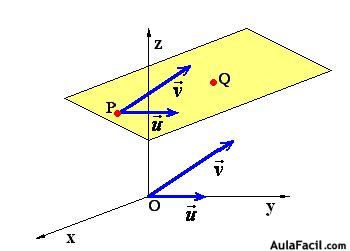
Ecuación de la recta dados 2 puntos

El plano en 3 dimensiones

Ecuación segmentaria del plano

Ecuación normal del plano

MIERCOLES 8 DE OCTUBRE

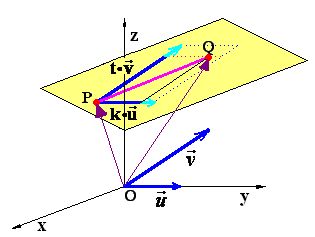
Plano determinado por 3 puntos

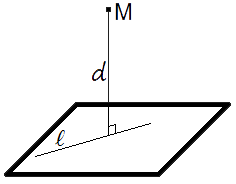
Distancia de un punto a un plano.

Recta determina por 2 planos.

Has de planos

MARTES 14 DE OCTUBRE

Ecuación vectorial de la esfera.

Caso particular x^2 + y^2 + z^2 = R^2 si el centro esta en el origen.

Superficies en 3 dimensiones.

Algunas superficies en 3 dimensiones son :
Paraboloides: circular, elíptico, hiperbólico
Cono elíptico
Hiperboloide: de una y dos hojas.

Análisis de las superficies en 3 dimensiones

Intersección con los ejes coordenados

Con el eje OX
Con el eje OY
Con el eje OZ

2. Intersección con los planos coordenados

Con el plano XOY
Con el plano XOZ
Con el plano YOZ

3. Intersección con los planos paralelos a los planos coordenados.

Paralelos al plano XOY
Paralelos al plano YOZ
Paralelos al plano XOZ

MIÉRCOLES 15 DE OCTUBRE.

En esta clase se realizó 1 ejercicio como práctica de lo aprendido dentro del tema de análisis de las superficies en 3 dimensiones.
El ejercicio fue :
x= y^2 - z^2.
También se realizó la corrección del deber anterior.
El ejercicio fue:
z = cos (x)

MARTES 21 DE OCTUBRE.

En este día se tomo la primera evaluación que constaba de los temas aprendidos en clase:

Los puntos que se evaluó fueron

Dados los puntos A(1,0,1) ; B(2,3,0) ; C(-1,1,4) y D(0,3,2) encuentre el volumen del paralelepípedo con aristas adyacentes AB, AC, AD.
La recta L1 pasa por el punto (1,1,1) y es paralela al vector, y una recta L2 que pasa por el punto (2,1,0) y es paralela al vector (3,8,13). Determine el punto de intersección de las 2 rectas.
Determine el vector unitario "n" perpendicular al plano que pasa por los puntos P(1,3,-2), Q(2,4,5), R(-3,-2,2).
Realizar el análisis gráfico de la superficie Z= exp - (x^2 + y^2).

MIÉRCOLES 22 DE OCTUBRE.

FUNCIONES VECTORIALES