Enero

MARTES 6 DE ENERO 
PUNTOS EXTREMOS
Máximos y mínimos
  1. Relativos.
  2. Absolutos
  3. Condicionales
Sea z= f(x,y) una función de 2 variable, se dice que f(x,y) tienen un máximo relativo en (a,b) si se cumple:  f(x,y)  ≥  f(a,b) cuando (x,y) se acerca a  (a,b).

ejemplos propuestos en clase de máximos y mínimos.
Un punto de silla es aquel punto donde f(x,y) presenta un máximo relativo con respecto a la variable y un mínimo relativo con respecto a la otra.
Criterio de la segunda derivada.
1.- Hallar las derivadas parciales fx, fy
2.- Hallar los puntos críticos  fx=0, fy=0
3.- Hallar las detrivadas parciales de segundo orden: fxx, fyy, fxy
4.- Determinar:

Ejercicios de aplicación de la segunda derivada.

MIÉRCOLES 7 DE ENERO

Mínimos y máximos absolutos.
La función f(x) presenta un máximo relativo en xo , cuando existe un entorno E(xo) tal que:

La función f(x) presenta un mínimo relativo en xo , cuando existe un entorno E(xo) tal que:
Son puntos que se distinguen por ser aquellos cuya imagen es la mayor o la menor (máximo - mínimo) de todas las imágenes “de los alrededores”. No se excluye que haya otros puntos "alejados" de xo cuya imagen sea mayor o menor que f(xo).
A los máximos y mínimos relativos se los llama extremos relativos o simplemente extremos.

Multiplicadores de Lagrange.

Para determinar los valores máximos y mínimos de f(x,y,z) sujeta a la restricción g(x,y,z)=k 
Determinar todos los valores de x,y,z y \lambda  tal que: 

\bigtriangledown f(x,y,z) = \lambda \bigtriangledown g(x,y,z)
g(x,y,z) = k

Ejemplo:
  • La función de producción de Cobb- Douglas para un cierto fabricante viene dada por f(x,y) = 100x^\frac{3}{4} y ^\frac{1}{4} donde x denota las unidades de trabajo (Q. 150.00 unidades) e y las unidades de capital (Q 250.00 la unidad) Hallar el máximo nivel de producción admisible para este fabricante, si tiene el coste conjunto de trabajo y capital limitado a Q50000.00
FO: 100x^\frac{3}{4} y ^\frac{1}{4}

FR: 150X+250Y=50000

fx= 75y^\frac{1}{4}x^\frac{-1}{4}
fy= 25x^\frac{3}{4}y^\frac{-3}{4}
\frac{75y^\frac{1}{4}x^\frac{-1}{4}= \lambda 150 }{25x^\frac{3}{4}y^\frac{-3}{4}=\lambda 250 }
x=5y

FR: 150(5y)+250y=50000
750y+250y=50000
y=50000/10000
y=50


MARTES 13 DE ENERO
Integrales múltiples.



Sumas de Riemann:

  • Integrales sobre regiones rectangulares.
  • Integrales sobre regiones mas generales.




MARTES 20 DE ENERO.

Transformación de integrales múltiples.

Coordenadas rectangulares a polares 


Coordenadas rectangulares a esféricas


Coordenadas rectangulares a cilíndricas.

Ejercicios de aplicación de integrales múltiples en volúmenes y áreas de superficies.

MIÉRCOLES 21 DE ENERO

 Ejercicios de aplicación de integrales múltiples en volúmenes y áreas de superficies.
Aplicación de integrales simples, dobles y triples para encontrar volúmenes y áreas de un mismo ejercicio y comprobar que  os da el mismo resultado.

Centro de masa.
Momento de inercia 

Aplicación de las formulas de centro de masa en ejercicios.

MARTES  27 DE ENERO

 Integrales de línea.

 Definición. Sea f : Ω → R un campo escalar continuo, con Ω ⊆ R n , y sea γ : [a,b] → Ω un camino regular a trozos. La integral de línea de f a lo largo de γ es:
por definición: Z γ f dl = Z b a f γ(t) kγ 0 (t)kdt

Definición. Sea ahora F : Ω → R n un campo vectorial continuo en un conjunto Ω ⊆ R n y γ : [a,b] → Ω un camino regular a trozos.
La integral de línea de F a lo largo de γ es, por definición: Z γ F.dl = Z b a F γ(t) γ 0 (t) dt La existencia de esta integral está asegurada por las mismas razones comentadas en el caso de un campo escalar

MIÉRCOLES 28 DE ENERO 

 Ejercicios de aplicación de las integrales de línea.
Se observó videos de las demostraciones de las integrales de linea.

Parametrización de la circunferencia.

 r= x^2 + y^2

x= rcos(x)
y=rsen(x)

SÁBADO 31 DE ENERO 

 Segunda prueba bimestral.

 MARTES 3 DE FEBRERO.

 Integrales de líneas en un campo vectorial.

 Ejercicios de aplicación de las integrales de línea, se observó una serie de videos sobre las demostraciones de las integrales de línea en un campo vectorial.

Relación entre integrales de líneas de los campos vectoriales y de los campos vectoriales.

 Ejercicios de aplicación relación entre integrales de líneas de los campos vectoriales y de los campos vectoriales.

MIÉRCOLES 4 DE FEBRERO

 Teorema de Green en el plano.

 Sea C una curva cerrada simple regular a trozos, positivamente orientada, en el plano R 2 , y sea D la unión de la región interior a C con la propia curva C. Sea F = (P, Q) : D −→ R 2 un campo vectorial de clase C 1 .



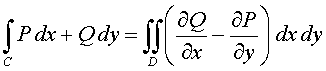
Ejercicios de aplicación del teorema de Green.

MARTES 10 DE FEBRERO

Examen final.


No hay comentarios:

Publicar un comentario

Suscribirse a: Comentarios (Atom)