Revisión del examen.
MIÉRCOLES 3 DE DICIEMBRE.
Ejercicios de aplicación de derivadas de orden superior.
Incrementos y diferenciales
Para funciones de una variable  , se define el incremento de
, se define el incremento de  como
como
y la diferencial de  como
como
En la siguiente figura se muestra  .
.

Observe que  se aproxima a cero más rápidamente que
se aproxima a cero más rápidamente que  , ya que
, ya que

y al hacer  , tenemos que
, tenemos que  .
.
Por tanto
donde  conforme
conforme  .
.
Ahora consideremos una función de dos variables
Si  y
y  son incrementados
son incrementados  y
y  , entonces el correspondiente incremento de
, entonces el correspondiente incremento de  es
es
Con lo cual  representa el cambio en el valor de
representa el cambio en el valor de  cuando
cuando  cambia a
cambia a  .
.
MARTES 9 DE DICIEMBRE.
Ejercicios de incrementos y diferenciales.
En un incremento la parte lineal principal indica el valor exacto, mientras que, la parte de infinitésimos de orden superior indican un valor aproximado.
.jpg)
Reglas de diferenciación.

Derivadas y diferenciales de funciones compuestas.
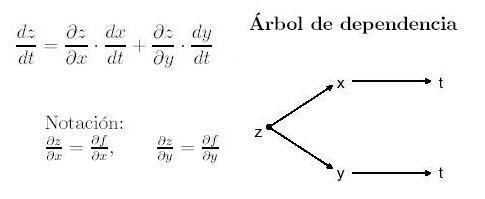








Ejercicios de incrementos y diferenciales.
En un incremento la parte lineal principal indica el valor exacto, mientras que, la parte de infinitésimos de orden superior indican un valor aproximado.
.jpg)
Reglas de diferenciación.

Derivadas y diferenciales de funciones compuestas.
MIÉRCOLES 10 DE DICIEMBRE.
Ejercicios de aplicación de las derivadas y diferenciales de funciones compuestas.

MARTES 16 DE DICIEMBRE.
Ejercicios de aplicación de las derivadas y diferenciales de funciones compuestas.
Derivación de funciones implícitas.
Estas funciones se pueden resolver por medio de 3 diferentes métodos.
1.- Por diferenciación.
2.- Por Jacobiano.
3.- Por derivación implícita.
Sistemas de funciones implícitas (se resuelven por los 3 anteriores métodos)
MIÉRCOLES 17 DE DICIEMBRE.
Ejercicios de sistemas de funciones implícitas por los 3 métodos.
Derivada direccional y vector gradiente.
Se llaman derivadas direccional de la función z = f(x,y) en un punto P(x,y) en el sentido del vector el siguiente límite si existe y es finito:
el siguiente límite si existe y es finito:
 el siguiente límite si existe y es finito:
el siguiente límite si existe y es finito:
Para calcular este límite se toma el vector unitario  de la dirección del vector
de la dirección del vector  (dividiéndolo por su módulo). Llamamos t a la longitud del vector
(dividiéndolo por su módulo). Llamamos t a la longitud del vector  , es decir
, es decir ,con lo cual
,con lo cual  , de donde
, de donde  , y el límite se reduce a la única variable t
, y el límite se reduce a la única variable t
 de la dirección del vector
de la dirección del vector  (dividiéndolo por su módulo). Llamamos t a la longitud del vector
(dividiéndolo por su módulo). Llamamos t a la longitud del vector  , es decir
, es decir ,con lo cual
,con lo cual  , de donde
, de donde  , y el límite se reduce a la única variable t
, y el límite se reduce a la única variable t
Si la función f(x, y) es diferenciable, entonces la derivada direccional se calcula por la fórmula:

(es decir la suma de los productos de las parciales por las componentes del vector unitario)
Si la función es de tres variables z=f(x, y, z) la derivada direccional se calcula de manera análoga:

(Las parciales habrá que calcularlas en el punto correspondiente. Las componentes del vector unitario coinciden con los cosenos directores del vector director. Si la función no es diferenciable esta fórmula no es válida y hay que calcular el límite anterior).
Se llama gradiente de una función z = f(x, y) en un punto P(x, y) al vector que sale del punto P y sus componentes son las derivadas parciales de la función en dicho punto

La derivada direccional se puede obtener como el producto escalar del gradiente por el vector unitario (si la función es diferenciable)

El gradiente indica el sentido de crecimiento más rápido de una función en un punto dado. La derivada direccional tiene su valor máximo en el sentido del gradiente y coincide con su módulo:

Si la función es de tres variables u = f(x, y, z) el gradiente se define de forma análoga:

No hay comentarios:
Publicar un comentario